Diffusion Models: Fundamentals - Part 1
Update history
- 20.12.2023: Created
- 02.01.2024: Update the math formulation
- 03.01.2024: Update the model backbone
- 04.01.2024: Update the implementation
What is Diffusion Model
- Motivation
- From VAE: the same concept but gradually
- From GAN: the same concept that generate from noise
- General concept
- Markov Chain with 2 stages: forward and reverse
- Forward process
- Reverse process
- Objective function
- Learn to generate the image from noise
- Compare
- to GAN: more stable in training
- to VAE:
General concept
The general objective is to gradually adding noise to the original image unitl it completely becames noise, and then try to generate back to the original image from the existing noise. By learning this process, a diffusion model is expected to learn how to generate an image from a noise distribution by learning the denoising process.
Diffusion model is a Markov Chain process with two stages: forward and reverse.
- Forward process:
- In the forward process, the objective is to adding noise to the image within finite steps until it completely becomes noise
- Reverse process:
- In the reverse process, the model learns to denoise from a noise distribution and generate back the original image within finite steps
- Objective function:
- Similar to VAE, diffusion model optimizes the evidence lower bound (ELBO), which means we want to maximize the log-likelihood between the original image and the generated one.
Math formulation
- We denote the real data distribution as \(q(x)\)
- A data point (real image) is sampled as \(\mathbf{x}_0 \sim q(\mathbf{x})\)
- The Markov chains is defined as \(T\) finite steps
Forward process
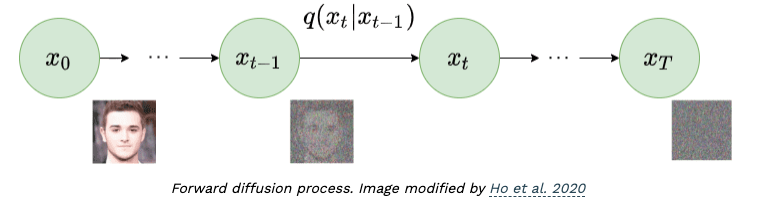
- In the forward process, at timestep t, we have the noised image \(\mathbf{x}_t\) by adding noise from a distribution (normally Gaussian) to the previous image \(\mathbf{x}_{t-1}\), this process is denoted as \(q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\)
Formally,
\[\begin{equation} \label{eq:original_q_forward} q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}) \end{equation}\]where \(\beta_{t}\) is a paramter to control the level of noise at timestep \(t\), \(\{\beta_t \in (0,1)\}_{t=1}^{T}\).
Thanks to the property of the Markov chain, we can create a tractable closed. Given \(\alpha_t = 1 - \beta_t\), \(\bar{\alpha_t} = \prod_{i=1}^{t} \alpha_i\), then
\[\begin{equation} \label{eq:closed_form} \begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t} \mathbf{x}_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-1} \\ &= \sqrt{1 - \alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar\epsilon_{t-2} \\ &= \dots \\ &= \sqrt{\bar\alpha_t} \mathbf{x}_0 + \sqrt{1 - \bar\alpha_t} \epsilon \end{aligned} \end{equation}\]On the above equation \eqref{eq:closed_form}, we denote \(\epsilon_t \in \mathcal{N}(0, \mathbf{I})\). \(\bar\epsilon_{t}\) is a merged Gaussian distribution.
From that, the closed form of forward process is defined as
\[\begin{equation} \label{eq:closed_form_forward} q(\mathbf{x}_t | \mathbf{x}_{0}) = \mathcal{N} \left( \mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_{0}, (1 - \bar{\alpha}_t) \mathbf{I} \right) \end{equation}\]Reverse process
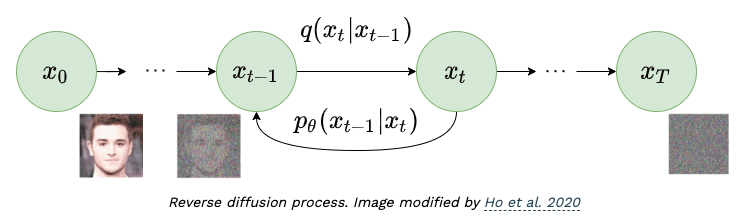
- Theoretically, the reverse process would be \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t})\).
- However, to find out the above distribution, we need to figure out the wholte data distribution, which is impractical
- The alternative is the reparameterizatin trick, sample from mean and distribution of the previous distribution. The approximation is \(p_{\theta}(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\).
- Because \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t})\) is a Gaussian distribution, with a small \(\beta_t\), \(p_{\theta}(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\). is also a Gaussian distribution, so we can sample using the above clarification.
Formally, \(\begin{equation} p_{\theta}(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N} \left( \mathbf{x}_{t}; \mathbf{\mu}_{\theta}(\mathbf{x}_t, t), \mathbf{\sum}_{\theta}(\mathbf{x}_t, t) \right) \end{equation}\)
Objective function
We optimize the ELBO function on the negative log-likelihod function.
\[\begin{equation} \begin{aligned} \mathbb{E}[-\log p_{\theta}(\mathbf{x_0})] &\leq \mathbb{E_q}[-\log \frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)}] \\ &= \mathbb{E_q}[-\log p(\mathbf{x}_T) - \sum_{t \geq 1} \frac{ p_{\theta}(\mathbf{x}_{t-1} \vert \mathbf{x}_t)} {q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})} ] \\ &=: L \end{aligned} \end{equation}\]Derive the above function, we get
\[\begin{equation} \label{eq:original_loss} L := \mathbb{E_q} \left[ \underbrace{D_{KL} \left( q(\mathbf{x}_T \vert \mathbf{x}_0) \enspace \vert\vert \enspace p_{\theta}(\mathbf{x}_T) \right) _ {L_T}} _{L_T} + \underbrace{\sum\limits_{t \geq 1} D_{KL} \left( q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t}, \mathbf{x}_{0}) \enspace \vert\vert \enspace p_{\theta}(\mathbf{x}_{t-1} \vert \mathbf{x}_{t}) \right) } _{L_{t-1}} - \underbrace{\log p_{\theta} (\mathbf{x}_0 \vert \mathbf{x}_1)} _{L_0} \right] \end{equation}\]In the above training loss, we observer there are three parts:
- \(L_T\) is a constant, and can be ignored during the training since \(q\) has no learnable parameters and \(\mathbf{x}_t\) is a Gaussian noise
- \(L_0\) is a reconstruction term and is learned using a seperate decoder following \(\mathcal{N} \sim (\mathbf{x}_0; \mu_\theta(\mathbf{x}_1, 1), \Sigma_\theta (\mathbf{x}_1, 1) )\)
- \(L_{t-1}\) is a learnable parameters and we focus on how to learn this subloss function.
In \(L_{t-1}\), the term \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t}, \mathbf{x}_{0})\) has not been defined. In words, it means we wish to denoise the image from previous noisy one \(\mathbf{x}_{t}\) and it is also conditioned on the original image \(\mathbf{x}_0\). As a result,
\[\begin{equation} \label{eq:original_reverse} q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t}, \mathbf{x}_{0}) \sim \mathcal{N}(\mathbf{x}_{t-1}, \tilde\mu_t(\mathbf{x}_{t}, \mathbf{x}_0), \tilde\beta_{t} \mathbf{I}) \end{equation}\]with
\[\begin{equation} \tilde\beta_t = \frac{1- \bar\alpha_{t-1}}{1 - \bar\alpha_t} \cdot \beta_t \end{equation}\]Using the Bayes rules, \(\tilde\mu_t(\mathbf{x}_t, \mathbf{x}_0)\) in Equation \eqref{eq:original_reverse} can be derived into
\[\begin{equation} \label{eq:original_mu_noise} \tilde\mu_t(\mathbf{x}_t, \mathbf{x}_0) = \frac{\sqrt{\bar\alpha_{t-1}} \beta_t}{1 - \bar\alpha_t} \mathbf{x}_0 + \frac{\sqrt\alpha_t (1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t} \mathbf{x}_t \end{equation}\]However, it still depends on two variables, \(\mathbf{x}_0\) and \(\mathbf{x}_t\), we want to transform it to only depends on one variable. Because we have a tractable closed-form of \(\mathbf{x}_0\) and \(\mathbf{x}_t\) and \(\epsilon_t \sim \mathcal{N}(0, \mathbf{I})\) in Equation \eqref{eq:closed_form}, the Equation \eqref{eq:original_mu_noise} becomes
\[\begin{equation} \label{eq:mu_noise} \tilde\mu_t(\mathbf{x}_t) = \frac{1}{\sqrt{\alpha_t}} ( \mathbf{x}_{t} - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}} \epsilon_t ) \end{equation}\]Recall the \(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\) derive formula in Equation \eqref{eq:original_loss}, we can have the same transformation with a learnable \(\epsilon_\theta(\mathbf{x}_t, t)\) for \(\mu_\theta(\mathbf{x}_t, t)\)
\[\begin{equation} \label{eq:mu_learnable_noise} \mu_\theta(\mathbf{x}_t, t) = \frac{1}{\sqrt{\alpha_t}} ( \mathbf{x}_{t} - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}} \epsilon_\theta(\mathbf{x}_t, t) ) \end{equation}\]From the above equation, we observe that the generated \(\mathbf{x}_t\) depends only on a trainable variable, which is \(\epsilon_\theta(\mathbf{x}_t, t)\), at timestep \(t\). The problem turns out to predict the noise of the generated image for every step \(t\) in the denoising process. As a result, we define a neural network to predict \(\epsilon_\theta(\mathbf{x}_t, t)\)
Applying \eqref{eq:mu_noise} and \eqref{eq:mu_learnable_noise} into the \(L_{t-1}\), now the objective is to minimize the difference between the current noise and the predicted noise
\[\begin{equation} \begin{aligned} L_{t} &= \mathbb{E}_{\mathbf{x}_0, \epsilon} \left[ \frac{1}{2 || \Sigma_\theta (\mathbf{x}_t, t) ||_2^2} || \tilde\mu_t(\mathbf{x}_t, \mathbf{x}_0) - \mu_\theta(\mathbf{x}_t, t) ||^2 \right] \\ &= \mathbb{E}_{\mathbf{x}_0, \epsilon} \left[ \frac{(1 - \alpha_t)^2}{2 \alpha_t (1 - \bar\alpha_t) || \Sigma_\theta ||_2^2} || \epsilon_t - \epsilon_\theta(\sqrt{\alpha_t} \mathbf{x}_0 + \sqrt{1 - \bar\alpha_t} \epsilon_t, t) ||^2 \right] \end{aligned} \end{equation}\]By discarding the regulaization term, Ho et al. proposed with a simpler version
Since we ignore the other parts of the overall loss function and with the simple version, the final loss function is
\[\begin{equation} L_{\text{simple}} = L_{t}^{\text{simple}} + C \end{equation}\]where \(C\) is a constant
Explanation for the impractical of \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t})\)
TODO
Explanation for the reparameterization trick
TODO
Bayes rule to expand the \(q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1}, \mathbf{x}_{0})\)
TODO
Overall training process
The process of developing diffusion model consitst of training and sampling.
Training
For each training step:
- Sample an original image from the dataset: \(\mathbf{x}_0 \sim q(\mathbf{x}_0)\)
- Sample range of timestep \(t\) in range (1, \(T\)), for example, sampling with a uniform: \(t \sim \text{Uniform}(\{1, \dots, T\})\)
- Sample noise: \(\epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)
- Calculate the gradient folllowing the loss function: \(\Delta_\theta || \epsilon - \epsilon_\theta(\sqrt{\alpha_t} \mathbf{x}_0 + \sqrt{1 - \bar\alpha_t} \epsilon_t, t)||^2\)
Sampling
The sampling process is when we want to generate the image from the noise distribution.
- First, we generate the noise: \(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)
- For each timestep from \(T\) to \(1\)
- Sample embedding from the noise distribution: \(\mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)
- Calculate the denoising version at timestep $t-1$ using the reparameterization trick:
- Get \(\mathbf{x}_0\)
The two process are summarized as follow Algorithms

Model backbone
Any model can be used as the backbone for a diffusion model. However, for the baseline Denoising Diffusion Probabilistic Model (DDPM), Ho et al.
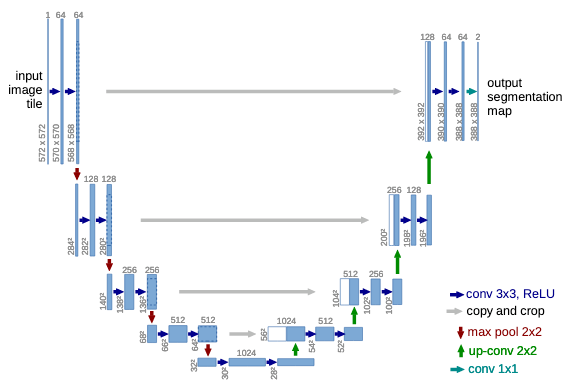
The advatange of U-Net architecture can be listed as follows:
- U-Net is a symetric architecture and is well-known for its application in segmentation. This means the architecture itself is potential for denoising tasks.
- The conventional structure of U-Net has encoder as the downsampling and decoder as the upsampling, with residual connection, which is similar to Auto-Encoder-based models.
- U-Net has many variants, the recent famous one is Attenion U-Net consisting of Wide Resnet blocks, Group Normalization, and Self-attention Blocks.
- However, to leverage the U-Net as the backbone, we need to differentiate between each timestep t. This can be resolved by using a Position Encoding. In
, the authors use SinusoidalPositionEmbeddings.
Summary
Implementation
Training process
Following the above algorithm
- Sample an original image from the dataset: \(\mathbf{x}_0 \sim q(\mathbf{x}_0)\).
- Sample range of timestep \(t\) in range \((1, T)\), for example, sampling with a uniform: \(t \sim \text{Uniform}(\{1, \dots, T\})\). In this step, we generate range of timestep with corresponding \(\beta_t\).
- Sample noise: \(\epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\). In this step, we sample noise and generate the noisy image at timestep \(t\) following Equation \eqref{eq:closed_form_forward}.
- Calculate the gradient folllowing the loss function: \(\Delta_\theta || \epsilon - \epsilon_\theta(\sqrt{\alpha_t} \mathbf{x}_0 + \sqrt{1 - \bar\alpha_t} \epsilon_t, t)||^2\). In this step, we calculate between the output of the model and the noisy image from the above step using Equation \eqref{eq:simple_loss_function}
As a result, in summary, we will implement the process as follow:
- Timestep and corresponding beta scheduler given number of steps
- Sample a noisy image at a timestep \(t\) with Equation \eqref{eq:closed_form_forward}.
- Define the loss function to calculate Equation \eqref{eq:simple_loss_function}
Timestep and beta scheduler
The importance of forward process is to define how we generate number of finite timestep in range \((0, T)\). The original DDPM paper uses the linear schedule for simple.
Recall Equation \eqref{eq:original_q_forward} with \(\beta_t\) as the parameter to control the level of noise. In the original implementation, the authors choose to scale linearly from \(\beta_1 = 10^{-4}\) to \(\beta_T = 0.02\). So we implement the same way.
We define linear_beta_schedule as the linear timestep scheduler with an input as the number of timesteps n_steps
def linear_beta_schedule(n_steps):
beta_start = 0.0001
beta_end = 0.02
return torch.linspace(beta_start, beta_end, n_steps)
We also need to prepare corresponding \(\alpha_t\) and \(\bar\alpha_t\). The following code prepare the list of alpha and utilization function to retrieve given timesteps
# define alphas
alphas = 1 - betas
cumprod_alphas = torch.cumprod(alphas, axis=0) # bar_alpha
# util function to retrive data at timestep t
def extract(data, t, out_shape):
"""Extract from the list of data the t-element and reshape to the given_shape
Args:
data (list or tensor): input list of tensor of data to retrieve
t (int): t element to retrieve data
out_shape (tuple): output shape
Returns:
tensor: retrieved data with dedicated shape
"""
batch_size = t.shape[0]
out = data.gather(-1, t.cpu())
return out.reshape(batch_size, *((1,) * (len(out_shape) - 1))).to(t.device)
Sample a noisy image at a timestep
Recall the Equation \eqref{eq:closed_form_forward}
\[q(\mathbf{x}_t | \mathbf{x}_{0}) = \mathcal{N} \left( \mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_{0}, (1 - \bar{\alpha}_t) \mathbf{I} \right)\]We implement a function to get noised image at any given timestep with given original image.
def sample_noised_image(x_start, timestep, noise=None):
"""Sample a noised image at a timestep
Args:
x_start (tensor): x0, original image
timestep (_type_): timestep t
noise (_type_, optional): noise type. Defaults to None.
"""
if noise is None:
noise = torch.randn_like(x_start)
cumprod_alpha_t = extract(cumprod_alphas, timestep, x_start.shape)
noised_t = (torch.sqrt(cumprod_alpha_t) * x_start) + (torch.sqrt(1 - cumprod_alpha_t) * noise)
return noised_t
Define the transform and inverse transform process
The transform process takes original image from PIL and transform to torch tensor data
image_size = 128
transform = Compose([
Resize(image_size),
CenterCrop(image_size),
ToTensor(), # turn into torch Tensor of shape CHW, divide by 255
Lambda(lambda t: (t * 2) - 1),
])
The inverse transform process convert the tensor data back to the PIL image
reverse_transform = Compose([
Lambda(lambda t: (t + 1) / 2),
Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
Lambda(lambda t: t * 255.),
Lambda(lambda t: t.numpy().astype(np.uint8)),
ToPILImage(),
])
Demo the forwarding process
Define the loss function
From Equation \eqref{eq:simple_loss_function}, we can apply any conventional function such as L1, MSE, etc. to calculate the different between noised image at timestep \(t\) and the predicted noise from the model.
def loss(denoise_model, x_start, timestep, noise=None, loss_type='mse'):
if noise is None:
noise = torch.randn_like(x_start)
x_noise = sample_noised_image(x_start, timestep, noise)
predicted_noise = denoise_model(x_start, timestep)
if loss_type == 'mse':
F.mse_loss(x_noise, predicted_noise)
else:
raise NotImplementedError()
return loss
The above code takes denoise_model into account, which is neural network that we will implement. The model will predict the noise at timestep \(t\) given the original image. In the next section, we will implement the model as the Attention U-Net.
Attention U-Net
There are modules we need to implement
- Positional Embeddings
- ResNet Block
- Attention Block
- Group Normalization
- Utils Blocks
Positional Embeddings
For each above timestep \(t\), we need to generate a positional embedding to differentiate between each timestep. The most common is to follow
class SinusodialPositionalEmbeddings(nn.Module):
def __init__(self, dim) -> None:
super().__init__()
self.dim = dim
def forward(self, timestep):
device = timestep.device
half_dim = self.dim // 2
embeddings = math.log(10000) / (half_dim - 1)
embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
embeddings = timestep[:, None] * embeddings[None, :]
embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
return embeddings
ResNet block
class Block(nn.Module):
"""A unit block in ResNet module. Each block consists of a projection module, a group normalization, and an activation
Args:
nn (_type_): _description_
"""
def __init__(self, in_dim, out_dim, groups=8, act_fn = nn.SiLU) -> None:
super().__init__()
self.proj = nn.Conv2d(in_dim, out_dim, 3, padding=1)
self.norm = nn.GroupNorm(groups, out_dim)
self.act_fn = act_fn()
def forward(self, x, scale_shift=None):
x = self.proj(x)
x = self.norm(x)
if scale_shift:
scale, shift = scale_shift
x = (x * (scale + 1)) + shift
x = self.act_fn(x)
return x
class ResNetBlock(nn.Module):
def __init__(self, in_dim, out_dim, *, time_emb_dim=None, groups=8, act_fn = nn.SiLU) -> None:
super().__init__()
self.mlp = (
nn.Sequential(
act_fn(),
nn.Linear(time_emb_dim, 2 * out_dim)
)
if time_emb_dim
else None
)
self.block1 = Block(in_dim, out_dim, groups, act_fn)
self.block2 = Block(out_dim, out_dim, groups, act_fn)
self.res_conv = nn.Conv2d(in_dim, out_dim, 1) if in_dim != out_dim else nn.Identity()
def forward(self, x, time_emb=None):
scale_shift = None
if self.mlp and time_emb:
time_emb = self.mlp(time_emb)
time_emb = rearrange(time_emb, "b c -> b c 1 1")
scale_shift = time_emb.chunk(2, dim=1)
h = self.block1(x, scale_shift)
h = self.block2(h)
return h + self.res_conv(x)
Attention Block
We follow the implementation of the paper
from torch import einsum
class Attention(nn.Module):
def __init__(self, dim, heads=4, head_dim=32) -> None:
super().__init__()
self.scale = head_dim * -0.5
self.heads = heads
hidden_dim = head_dim * heads
self.qkv_proj = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
self.out_proj = nn.Conv2d(hidden_dim, dim, 1)
def forward(self, x):
b, c, h, w = x.shape
qkv = self.qkv_proj(x).chunk(3, dim=1)
q, k, v = map(
lambda t : rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q * self.scale
sim = einsum("b h d i, b h d j -> b h i j", q, k)
sim = sim - sim.amax(dim=-1, keepdim=True).detach()
attn = sim.softmax(dim=-1)
out = einsum("b h i j, b h d j -> b h i d", attn, v)
out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
return self.out_proj(out)
Group Normalization
class GNorm(nn.Module):
def __init__(self, dim, fn) -> None:
super().__init__()
self.fn = fn
self.groupnorm = nn.GroupNorm(1, dim)
def forward(self, x):
x = self.groupnorm(x)
x = self.fn(x)
return x
Utils Blocks
Residual
class Residual(nn.Module):
def __init__(self, fn) -> None:
super().__init__()
self.fn = fn
def forward(self, x, *args, **kwargs):
return self.fn(x, *args, **kwargs) + x
Downsample block
class Downsample(nn.Module):
def __init__(self, in_dim, out_dim=None) -> None:
super().__init__()
out_dim = out_dim if out_dim is not None else in_dim
self.down_mlp = nn.Sequential(
Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),
nn.Conv2d(in_dim * 4, out_dim, 1),
)
def forward(self, x):
return self.down_mlp(x)
Upsample block
class Upsample(nn.Module):
def __init__(self, in_dim, out_dim=None) -> None:
super().__init__()
out_dim = out_dim if out_dim is not None else in_dim
self.up_mlp = nn.Sequential(
nn.Upsample(scale_factor=2, mode='nearest'),
nn.Conv2d(in_dim, out_dim, 3, padding=1)
)
def forward(self, x):
return self.up_mlp(x)
The whole model
class AttUNet(nn.Module):
def __init__(self, dim,
init_dim = None,
out_dim = None,
dim_mults=(1, 2, 4, 8),
channels=3,
self_condition=False,
resnet_block_groups=4) -> None:
super().__init__()
self.channels = channels
self.self_condition = self_condition
input_channels = channels * (2 if self_condition else 1)
init_dim = init_dim if init_dim is not None else dim
self.init_conv = nn.Conv2d(input_channels, init_dim, 1, padding=0)
dims = [init_dim, *map(lambda m : dim * m, dim_mults)]
in_out = list(zip(dims[:-1], dims[1:]))
block_klass = partial(ResNetBlock, groups=resnet_block_groups)
# positional embedding
time_dim = dim * 4
self.time_mlp = nn.Sequential(
SinusodialPositionalEmbeddings(dim),
nn.Linear(dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim)
)
# layers
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out)
for ind, (in_dim, out_dim) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1)
self.downs.append(
nn.ModuleList([
block_klass(in_dim, in_dim, time_emb_dim=time_dim),
block_klass(in_dim, in_dim, time_emb_dim=time_dim),
Residual(GNorm(in_dim, Attention(in_dim))),
Downsample(in_dim, out_dim) if not is_last else nn.Conv2d(in_dim, out_dim, 3, padding=1),
])
)
mid_dim = dims[-1]
self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
self.mid_attention = Residual(GNorm(mid_dim, Attention(mid_dim)))
self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
for ind, (in_dim, out_dim) in enumerate(reversed(in_out)):
is_last = ind == (len(in_out) - 1)
self.ups.append(
nn.ModuleList([
block_klass(out_dim + in_dim, out_dim, time_emb_dim=time_dim),
block_klass(out_dim + in_dim, out_dim, time_emb_dim=time_dim),
Residual(GNorm(out_dim, Attention(out_dim))),
Upsample(out_dim, in_dim) if not is_last else nn.Conv2d(out_dim, in_dim, 3, padding=1),
])
)
self.out_dim = out_dim if out_dim is not None else channels
self.final_res_block = block_klass(dim * 2, dim, time_emb_dim=time_dim)
self.final_conv = nn.Conv2d(dim, self.out_dim, 1)
def forward(self, x, timestep, x_self_cond=None):
if self.self_condition:
x_self_cond = x_self_cond if x_self_cond is not None else torch.zeros_like(x)
x = torch.cat((x_self_cond, x), dim=1)
x = self.init_conv(x)
r = x.clone()
t = self.time_mlp(timestep)
h = []
for block1, block2, attn, downsample in self.downs:
x = block1(x, t)
h.append(x)
x = block2(x, t)
x = attn(x)
h.append(x)
x = downsample(x)
x = self.mid_block1(x, t)
x = self.mid_attention(x)
x = self.mid_block2(x, t)
for block1, block2, attn, upsample in self.ups:
x = torch.cat((x, h.pop()), dim=1)
x = block1(x, t)
x = torch.cat((x, h.pop()), dim=1)
x = block2(x, t)
x = attn(x)
x = upsample(x)
x = torch.cat((x, r), dim=1)
x = self.final_res_block(x, t)
x = self.final_conv(x)
return x